Archangel: Graph Matching algorithm for Angel-Mortal-type games

Saturday. September 29, 2018 - 5 mins

Link To Project

GitHub page for Archangel.

Summary

An “Angel-Mortal” game is a gift-giving game played by a number of participants over a few weeks. The point of the game is for participants to give gifts to people and also be given gifts from people - essentially a circle of goodwill.

The Archangel project is a fun little piece of software I developed to facilitate the organization of these games (because it’s actually a hard CS problem!). It can be found at my GitHub page for Archangel.

Here, I’m going to try to explain why it’s necessary and exactly how it solves this seemingly trivial problem.

---

Formally defining the game and its rules

1. There are n participants.
2. Each participant has exactly 1 angel and 1 mortal.
3. A participant must not be told who their angel is. They must be told who their mortal is.
4. If participant A is participant’s B’s angel, it necessarily follows that participant A’s mortal is participant B, and participant B is not supposed to know that participant A is their angel.
5. A participant is supposed to give gifts to their mortal over the period of the game; these rules may vary across instances of the game.

The (base) problem

Given a list of participants, how can we generate a list of participants where every participant has an angel and mortal?

This basic version of the problem has a trivial solution.

1. Pick the first participant (i = 1) from the list - call this participant the origin
2. Pick the next participant (i = 2) from the list and make this participant the mortal of participant 1. This automatically means that participant 2’s angel is participant 1.
3. Continue until we reach the nth participant in the list. Participant n will be the mortal of participant n-1.
4. Finally, we create a closed loop by assigning participant 1 to be participant n’s mortal.

If we had 4 participants, we should be able to generate a graph like this:

Image Source

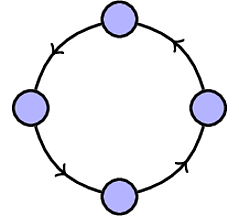
As a convention, when there is an arrow from A to B, this implies that B is A’s mortal.

The context surrounding Archangel

Archangel was deployed for continually for > 3 years (2015-now) in Tembusu College (in the National University of Singapore), where playing this angel-mortal game within the College is a tradition.

Clearly, the problem is not interesting given only the formal rules above. The context surrounding how the game was played in Tembusu meant that we had different optimization objectives: we wanted to promote getting to know people that are as unrelated from you as possible, among other things. This meant…

Constraints

We added constraints on exactly which two people could form an angel-mortal pair.

1. Two people that were from the same “house” (a.k.a. in the same group of floors) are not a valid angel-mortal pair. People are more likely to know other people from the same “house”, so this restriction was added.
2. Two people that are in the same faculty in NUS are not a valid angel-mortal pair, for the same reason.
3. Participants are allowed to specify a gender preference for their angel/mortal. This should be respected (e.g. if participant 1 requests for a male mortal, they should be allocated one). They can also indicate that they have no preference.

Representation of the participant chain and framing the solution

As seen before, we can represent the final output of this algorithm as a graph. However, we can also represent the initial state of the participant set as a graph - where each vertex is a participant, and an edge between two participants indicates a valid angel-mortal pairing. Such a graph might be very edge-heavy, and may look something like this.

Image Source

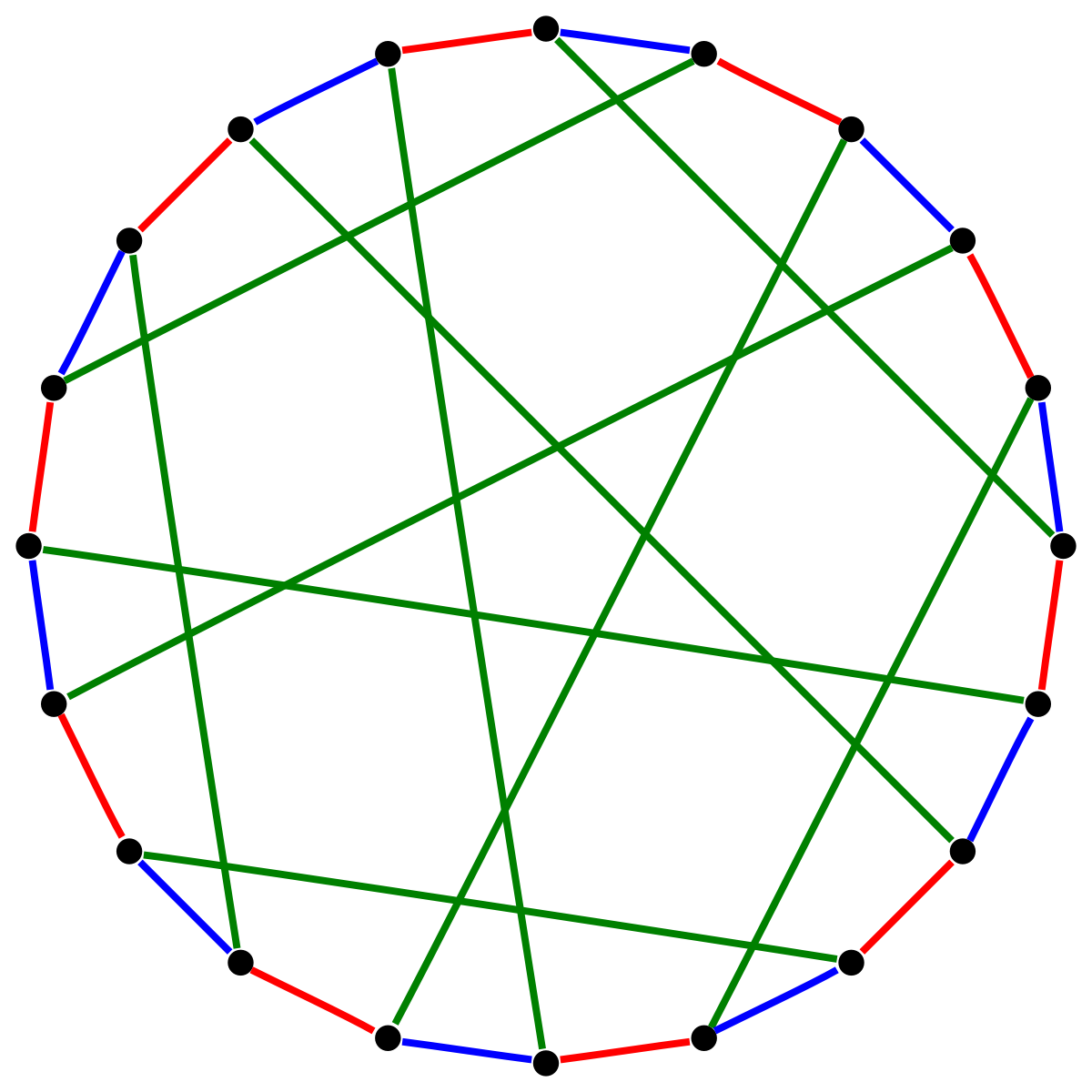
A valid solution is one where we have a path starting at some vertex that passes through all other vertices and ends back at the initial vertex, also known as the Hamiltonian path problem.

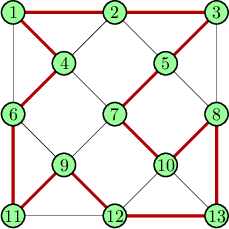
Here, the path is easy to see - just follow the outer circle. We may have to work much harder for a more complex graph. The picture below shows a valid Hamiltonian cycle for a given graph.

Image Source

Complexity, and how to generate the solution

Unfortunately, finding a Hamiltonian Cycle from an arbitrary graph is NP Complete. I didn’t want to give up on being able to generate a perfect solution, so I bit the bullet and decided to just roll with it - I was hoping that the small numbers of participants (< 400) would make the solution tractable.

Finding the solution then is easy, if not efficient. Just find a cycle of length n + 1 in the graph and we have a Hamiltonian circuit. This can be achieved through a depth-first search, backtracking every time we see a cycle that is less that length n + 1.

Code

I used python and the networkx library to do this. A participants.tsv (tab-separated values) file is read in by the program, which must follow a particular format with the participants data inside (likely from a Google Form). The initial graph is generated, then the Hamiltonian cycle is extracted if there is one. The final chain is written to an output file that can be used for the rest of the game.

Adjustments over the years

1. The 3 constraints that were discussed earlier can be relaxed by a percentage factor if no Hamiltonian cycle is being found. This makes it possible to actually generate a full chain.
2. The very first iteration of this program didn’t even use graphs - it just randomly created a chain and then gave the whole chain a “score” based on some terribly-chosen compatibility numbers. It then repeated the process millions of times and then chose the best chain (in this iteration we were also trying to match people based on their interests by keywords - it didn’t go well). Suffice to say that iteration is best forgotten.

Current Status

The Archangel algorithm is still being used and continues to be improved upon.

---